Reference electrode potentials

Figure 1: Equilibrium potentials at \(\SI{25}{\degreeCelsius}\) for some commonly used reference electrodes. Reproduced from Roberge (2008).

Figure 2: Graphical comparison of some common reference electrode potential scales. Of course, the scales are going “the wrong way” (we like negative to be up). (Roberge 2008, 67)

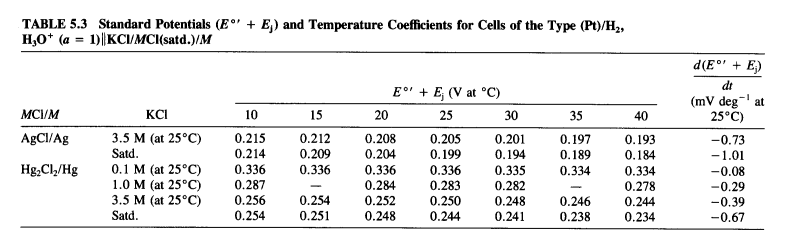
Figure 3: Standard potentials of silver-silver chloride and calomel electrodes at various electrolyte concentrations and temperatures. Reproduced from (Sawyer, Sobkowiak, and Roberts 1995, 192).

The absolute potential scale

Figure 4: Conversion of relative reference electrode potentials into electronic energies for aqueous systems. Reproduced from Trasatti (1986).

Trasatti (1986) shows a calculation of the absolute potential of SHE in water and recommends the following conversion:

\[\begin{equation} E^\circ(\ce{H+}/\ce{H2})^{\ce{H2O}}\text{(abs)} = \SI{4.44+-0.02}{\volt}\quad\mathrm{at}~\SI{298.15}{\kelvin} \end{equation}\]

It is to be noted that the uncertainty in the knowledge of \(E^\circ(\ce{H+}/\ce{H2})\text{(abs)}\) (\(\SI{+-20}{\mV}\)) by far exceeds the accuracy of most measurements of electrode potentials. Therefore, any convenience in the use of the absolute potential scale is confined to the specific cases when calculations of electronic energy levels are needed.

— Trasatti (1986)

On this topic there is also an interesting discussion in Morrison (1980), p. 31.

I did a quick scan of all papers that cite Trasatti (1986), and found no more recent recommendation on the relation between SHE and AVS. For now we will stick with Trasatti’s value.

The precise relation between the potential of a free electron in vacuum (absolute vacuum scale) and the conventional standard hydrogen electrode scale for aqueous solutions is still debated. (Inzelt, Lewenstam, and Scholz 2013)

Notes

[…] mercury-containing REs (calomel or mercury–mercuric oxide) are inappropriate for measurements in conjunction with platinum electrodes, since the mercury ions readily poison platinum surfaces.

— (Bagotsky 2006, 195)

If this is a rule, we break it quite often.

Convert to or from any* electrode scale

Having the the conversion algorithm in its own package like this should make the codebase easier to maintain and improve going forward. If you have any suggestions or comments regarding the data or the code of this package please don’t hesitate to open an issue or pull request on Github. I would be very grateful to hear any feedback.

* Any here denotes any one of the reference electrode scales that the refelectrodes package currently supports:

• AgCl/Ag in saturated NaCl(aq) at RT, in saturated KCl(aq) from \(\SIrange{10}{40}{\degreeCelsius}\), and in \(\SI{3.5}{\mol\per\litre}\) KCl(aq) from \(\SIrange{10}{40}{\celsius}\),
• Hg₂Cl₂/Hg in saturated KCl(aq) from \(\SIrange{10}{40}{\celsius}\), in \(\SI{3.5}{\mol\per\litre}\) KCl(aq) from \(\SIrange{10}{40}{\celsius}\), in \(\SI{1.0}{\mol\per\litre}\) KCl(aq) from \(\SIrange{10}{40}{\celsius}\), and in \(\SI{0.1}{\mol\per\litre}\) KCl(aq) from \(\SIrange{10}{40}{\celsius}\),
• SHE (it is zero at all temperatures and concentrations by definition),
• Li at RT,
• Na at RT,
• Mg at RT, and
• the absolute vacuum scale at RT.

This data is defined in the potentials.as.SHE() function which constitutes the core of the refelectrodes package.

As for the conversion functions, those are the aptly named as.SHE() which converts from any reference electrode scale to SHE, and from.SHE() which converts from SHE to any of the other scales.

The package also exports RefCanonicalName() which is a convenience function that allows the user to specify the name of each reference electrode scale using any of its common names. And that is effectively the extent of the package. ¹

Let’s take a quick walk through loading this package and testing its functions. You will want to start by installing and loading the package:

remotes::install_github("solarchemist/refelectrodes")
library(refelectrodes)
# I suggest you load these packages if you want to replicate the plot below
library(knitr)
library(ggplot2)
library(ggrepel)
library(dplyr)
library(magrittr)

The core function defines the dataset and when run will happily return this data as a tidy dataframe (this chunk shows just an excerpt of the tibble):

potentials.as.SHE() %>%
   group_by(electrode, electrolyte) %>%
   arrange(SHE) %>%
   # return first and last row (if any) within each group
   filter(row_number() %in% c(1, n())) %>%
   arrange(electrode, SHE)
## # A tibble: 11 × 9
## # Groups:   electrode, electrolyte [8]
##    electrode electrolyte conc.num conc.string   temp    SHE sid   reference     dEdT
##    <chr>     <chr>          <dbl> <chr>        <dbl>  <dbl> <chr> <chr>        <dbl>
##  1 AgCl/Ag   "KCl(aq)"        4.2 "saturated"    40   0.184 2     Sawyer19… -1.00e-3
##  2 AgCl/Ag   "KCl(aq)"        3.5 "3.5M at 25…   10   0.215 1     Sawyer19… -7.36e-4
##  3 AgCl/Ag   "NaCl(aq)"       5.9 "saturated"    25   0.263 9     CRC 97th… NA      
##  4 AVS       ""              NA   ""             25  -4.44  7     Trasatti… NA      
##  5 Hg2Cl2/Hg "KCl(aq)"        4.2 "saturated"    40   0.234 6     Sawyer19… -6.64e-4
##  6 Hg2Cl2/Hg "KCl(aq)"        0.1 "0.1M at 25…   25   0.336 3     Sawyer19… -7.86e-5
##  7 Li        ""               1   "1.0M at 25…   25  -3.04  10    CRC 97th… NA      
##  8 Mg        ""               1   "1.0M at 25…   25  -2.37  12    CRC 97th… NA      
##  9 Na        ""               1   "1.0M at 25…   25  -2.71  11    CRC 97th… NA      
## 10 SHE       ""              NA   ""           -273.  0     8     Inzelt20…  0      
## 11 SHE       ""              NA   ""            580   0     8     Inzelt20…  0

The dataframe is tidy, so more data can easily be added to this dataset by adding more rows.

Now, some of the the columns of this dataframe warrant some explanation. potentials$electrode is the name of the reference electrode, as defined by the function RefCanonicalName() (see below). potentials$conc.string was added so that the user does not need to remember the saturation concentration for various salts in solution. And for those unsaturated electrolytes it was a good place to put information on the temperature where the concentration was defined. Saturation does not depend on temperature, but the concentration of an unsaturated solution (expressed as amount/volume) does depend on temperature due to liquid expansion. Temperature and concentration values need no further explanation. potentials$setid is mainly for housekeeping - a simple way to keep track of the datasets in the dataframe (allows us to avoid having to resort to advanced matching against several parameters to later identify a particular set).

Note that no conversion happens in the potentials.as.SHE() function above. It just returns data.

Conversion is handled by the two functions as.SHE() and from.SHE(). The take the following arguments: the potential value (in volt), the scale (for the scale you want to convert from in the case of as.SHE(), and the one you want to convert to in the case of from.SHE()), and optional arguments for concentration and temperature (set to saturated and RT by default). The last argument expects the dataframe generated by potentials.as.SHE.

This way, all three of these functions are reasonably modular, and each one does a fairly well-defined job.

Some special considerations which are handled by these functions are perhaps worth mentioning here:

• concentration may be a number or a character string, which means we need to compare it to the appropriate column in the dataset,
• the temperature requested by the user may coincide with a datapoint in the dataset (in that case we just return that potential), otherwise we interpolate (by linear regression) based on the existing data,
• and for the final calculation of potential in SHE scale, we need to handle electronic (vacuum) and electrochemical scales separately because they go in opposite directions (this is handled by the ifelse(df$vacuum[p], ...) call.

The current implementation requires concentration to match an existing value. A functionality that could (perhaps even should) be added is the ability to interpolate concentrations in the same way as temperature (unless the change in potential with changing concentration deviates strongly from linearity).

Plotting the dataset

ggplot(potentials.as.SHE() %>%
          filter(electrolyte == "KCl(aq)")) +
   facet_wrap(~ electrode, ncol = 2) +
   geom_line(aes(x = temp, y = SHE, colour = conc.string)) +
   geom_point(aes(x = temp, y = SHE, colour =  conc.string)) +
   geom_text_repel(data = subset(potentials.as.SHE(), electrode != "AVS" & temp == 30),
                   aes(y = SHE, x = temp, label = conc.string, colour = conc.string),
                   point.padding = unit(0.25, 'lines'),
                   # hide the line connecting datapoint and label
                   segment.color = "transparent") +
   scale_y_reverse() +
   labs(x = expression("T/"*degree*C), # "T/C",
        y = "E/V vs SHE") +
   theme(legend.position = "none")

Figure 5: Electrode potentials vs SHE for the two reference electrodes in the dataset using \(\ce{KCl(aq)}\) electrolyte (each panel shows one reference electrode, each line shows a different electrolyte concentration). Just to demonstrate the extent of the dataset in parameter space.

Bibliography

• Reference Electrode Potentials - eDAQ wiki
• Conversion between reference electrodes - Corrosion Doctors

SessionInfo

## R version 4.0.5 (2021-03-31)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 18.04.6 LTS
## 
## Matrix products: default
## BLAS:   /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.7.1
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.7.1
## 
## locale:
##  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
##  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
##  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
## [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
## [1] refelectrodes_0.0.0.9000 common_0.0.2             magrittr_2.0.2          
## [4] dplyr_1.0.8              ggrepel_0.9.1            ggplot2_3.3.5           
## [7] knitr_1.37              
## 
## loaded via a namespace (and not attached):
##  [1] Rcpp_1.0.8       bslib_0.3.1      compiler_4.0.5   pillar_1.7.0    
##  [5] jquerylib_0.1.4  tools_4.0.5      digest_0.6.29    jsonlite_1.7.3  
##  [9] evaluate_0.14    lifecycle_1.0.1  tibble_3.1.6     gtable_0.3.0    
## [13] pkgconfig_2.0.3  rlang_1.0.1      DBI_1.1.2        cli_3.2.0       
## [17] yaml_2.2.2       blogdown_1.7     xfun_0.29        fastmap_1.1.0   
## [21] withr_2.4.3      stringr_1.4.0    generics_0.1.2   sass_0.4.0      
## [25] vctrs_0.3.8      tidyselect_1.1.2 grid_4.0.5       glue_1.6.1      
## [29] R6_2.5.1         fansi_1.0.2      rmarkdown_2.11   bookdown_0.24   
## [33] purrr_0.3.4      scales_1.1.1     htmltools_0.5.2  ellipsis_0.3.2  
## [37] assertthat_0.2.1 colorspace_2.0-2 utf8_1.2.2       stringi_1.7.6   
## [41] munsell_0.5.0    crayon_1.5.0